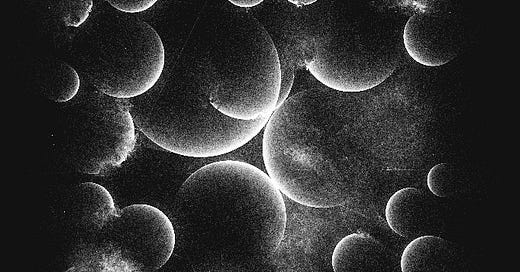
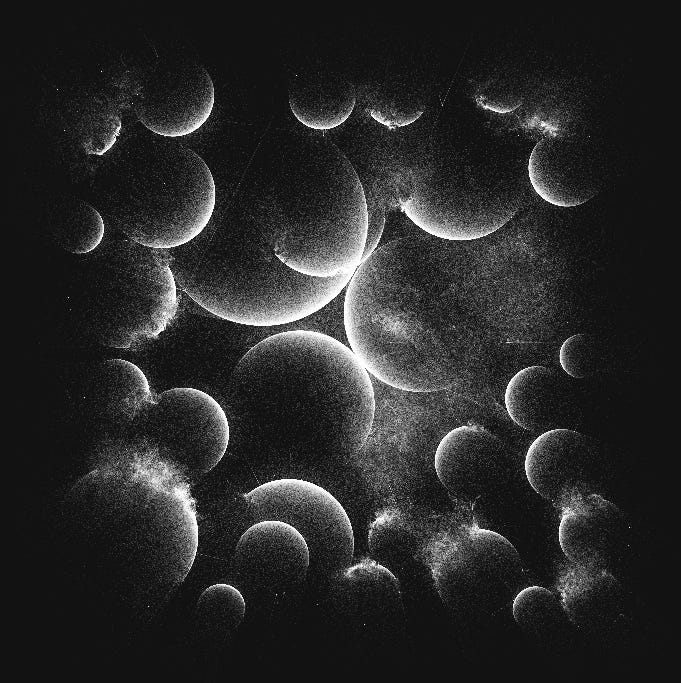
🔭 Breaking Down lunarean's Heat Death
Let's take a look at this masterpiece and try to figure out how it was done
Hello everyone!
Today I’m trying something different. I’ve been saying we should pay more attention to the coding side of gen art, and I found the perfect collection to take the first step.
Lunarean released Heat Death as part of fxhash interactive minting experience at The Ever-Evolving World of Art, Art Basel Hong-Kong, 2022. The code was left unmodified, which means it is open to the public.
Access the code here → https://gateway.fxhash2.xyz/ipfs/QmbXCxAvSDdhcyHEEhrdcD6cpduuQqNZHpntkD55e7hf2i/heatdeath.js
Interesting facts:
There are less than 180 lines of code. This was accomplished by simplifying multiple operations in one line as much as possible. E.g., using ? operator.
Five main functions:
setup: takes care of the background, canvas size, and coloring options.
Draw: uses the custom functions to draw the planets in a loop.
Calculate circles: creates the planets (circles), sizes, and positioning.
Draw points (take circles as input): forms the planets and the different effects using points.
Calculate theta: this controls the lightning directions.
880 outputs.
Five features: Palette, Mode, Margin, Full House, Tight.
Palettes: Dust, Plum, Picnic, Home, Calm.
Mode: Journey, Compass, Nest. This controls the lightning effect.
Margin: true/false,
Full House: true/false. Full house means it will continue generating planets until they don’t fit anymore.
Tight: true/false. No space between planets, so they are touching each other when true.
I broke the code into small sections and tried to explain what each part does. I asked lunarean some questions to clear some doubts about his logic and decisions.
p5.js documentation was linked for most functions to make it easier to follow.
Palette Selection
const PALETTES = [
{ name: "Dust", colors: ["#555555"] },
{ name: "Plum", colors: ["#513B56"] },
{ name: "Picnic", colors: ["#FAFAFA", "#0078BF", "#FF665E", "#FFCB47"] },
{ name: "Home", colors: ["#755B7B", "#77A0A9", "#F2545B", "#555555"] },
{ name: "Home", colors: ["#755B7B", "#77A0A9", "#F2545B", "#555555"] },
{ name: "Calm", colors: ["#447DC2", "#3B668C", "#E08D79", "#204344"] },
{ name: "Calm", colors: ["#447DC2", "#3B668C", "#E08D79", "#204344"] },
];
const palette = PALETTES[Math.floor(fxrand() * PALETTES.length)];
The Home and Calm palettes were included twice, so they have twice the chance of showing up.

Random seed initialization
const seed = Math.floor(fxrand() * 1e9);
randomSeed(seed);
noiseSeed(seed);
This is a clean way of initializing randomSeed, noiseSeed, and fxrand. You can use the p5.js random function and maintain deterministic outputs this way.
1e9 is just a simple way of using a big integer for the operation.
General Setup
const size = min(windowWidth, windowHeight);
createCanvas(size, size);
colorMode(HSB, 360, 100, 100, 1);
pixelDensity(2);
background(random(6, 10));
blendMode(SCREEN);
loop();
noStroke();
Using unique color interpretations mechanism - pixelDensity set to 2, blindMode(SCREEN), and colorMode set to HSB.
Parameters for the custom functions
// params for calcCircles()
numAttempts = isFullHouse ? 10000 : 25 * exp(sqrt(random()) * log(5));
minR = 0.03 * exp(log(3) * sqrt(random()));
maxR = minR * exp(log(3) * sqrt(random()));
sdBounds = 0.2 * exp(random(log(2)));
circleSpacing = isTight ? 1 : exp(sq(random()) * log(2));
overlapProb = 0.05 * sqrt(random());
margin = isMargin ? random(0.02, 0.12) : -1;
// params for drawPoint()
vignette = random(0.1, 0.5);
thetaSd = lerp(0.6, 0.9, sq(random())) + (random() < 0.05 ? 0.3 : 0);
meanBeams = sqrt(random());
scatterProb = 0.1 * sqrt(random());
umbraProb = 0.25 * sqrt(sqrt(random()));
saturationMod = random(0.5, 0.8);
brightnessMod = random(0.5, 0.8);
// params for calcTheta()
journeyNoise = random() < 0.8 ? 3 : 0;
journeyTheta = (int(random(12)) * TWO_PI) / 12;
compassSides = random() < 0.8 ? 4 : 6;
circles = calcCircles();
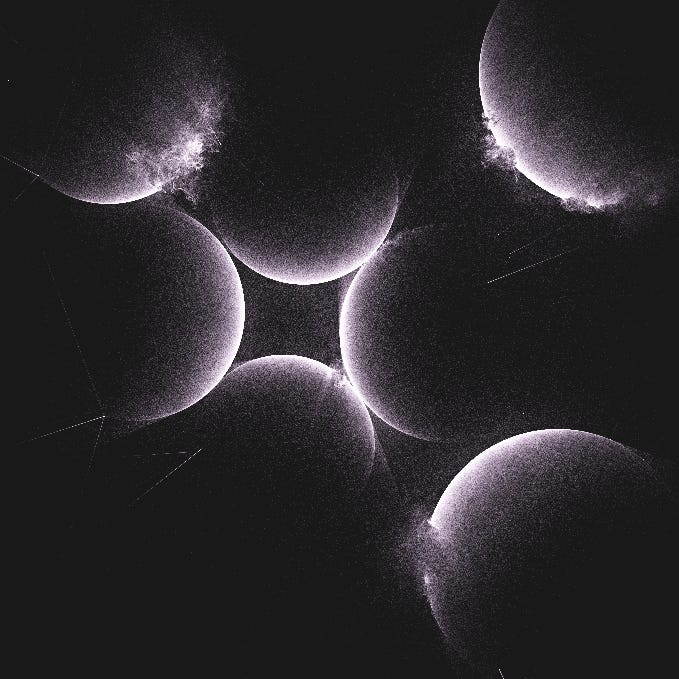
calcCircles Function
function calcCircles() {
const circles = [];
for (let i = 0; i < numAttempts; i++) {
// try to place some near center
const sd = map(i, 0, 100, 0.1, 0.25);
const x = i < 100 ? 0.5 + sd * randomGaussian() : random();
const y = i < 100 ? 0.5 + sd * randomGaussian() : random();
// perturb bounds so we don't end up with many circles the same size
let r = maxR * exp(sdBounds * randomGaussian());
// no overlap with center or edge
r = min(r, dist(x, y, 0.5, 0.5), x - margin, 1 - margin - x, y - margin, 1 - margin - y);
circles.map((c) => {
const skip = r > 0.1 && random() < overlapProb;
r = skip ? r / 2 : min(r, dist(x, y, c.x, c.y) - c.r * circleSpacing);
});
// only keep circle if it's big enough
if (r > minR * exp(sdBounds * randomGaussian())) {
const theta = calcTheta(x, y);
const sc = color(random(palette.colors));
const pointsLeft = ceil(25000000 * sq(r));
circles.push({ x, y, r, theta, sc, pointsLeft });
}
}
return shuffle(circles).sort((a, b) => brightness(a.sc) - brightness(b.sc));
}
This method calculates each circle (planet) and pushes them to an array. For each circle, it also calculates a theta variable (see calcTheta below).
To calculate the circle positions, lunarean used circle packing with his own variations.
By reading the comments, we can see how the algorithm tries to position planets in the center and avoids overlaps and small planets.
pointsLeft stores how many points should be drawn for that planet and is proportional to the area.
drawPoint Function
function drawPoint({ x, y, r, theta, sc }) {
const numBeams = round(meanBeams * exp(randomGaussian()));
// choose random chord
let theta1 = theta + thetaSd * randomGaussian();
let theta2 = theta + thetaSd * randomGaussian();
// specks and light beams
if (random() < 0.05 * numBeams) {
theta1 = theta2 = 1000 * noise(x, y, int(random(numBeams)));
// interior beam
if (random() < 0.1) {
theta1 *= 2;
}
}
// choose random point on the random chord
const w = random();
const isScatter = random() < scatterProb;
const scatterR = r * (isScatter ? 1 + 0.2 * exp(randomGaussian()) : 1);
let px = x + scatterR * lerp(cos(theta1), cos(theta2), w);
let py = y + scatterR * lerp(sin(theta1), sin(theta2), w);
// smoke warp. add x and y to avoid lining up between circles
let sa = lerp(noise(4 * px + 1000 * x, 4 * py + 1000 * y, 1), noise(40 * px, 40 * py, 2), 0.1);
sa = 3 * max(sa - 0.53, 0);
const ss = 150 * exp(noise(30 * px, 30 * py, 3) - 0.5);
const [px_, py_] = [px, py];
px += sa * (noise(ss * px_, ss * py_, 4) - 0.5);
py += sa * (noise(ss * px_, ss * py_, 5) - 0.5);
// jump in direction away from light source
if (random() < umbraProb) {
const umbraR = random(random(0.15));
const umbraTheta = calcTheta(px, py) + PI;
px += umbraR * cos(umbraTheta);
py += umbraR * sin(umbraTheta);
}
px += 0.0001 * randomGaussian();
py += 0.0001 * randomGaussian();
// build color
const edgeDist = min(px, 1 - px, py, 1 - py);
const vignetteMod = map(constrain(edgeDist, 0, 0.2), 0, 0.2, vignette, 1);
const s = saturationMod * saturation(sc);
let b = brightnessMod * vignetteMod * min(30, brightness(sc));
// blemishes
b *= 1 + 0.8 * (noise(30 * px, 30 * py, 3) - 0.5);
fill(color(hue(sc), s, b));
ellipse(px * width, py * height, 2 * 0.00025 * width, 2 * 0.00025 * height);
}
drawPoint takes a planet as input and “paints” an ellipse.
The smoky texture is based on domain warping.
“The shading on the planets is something I came up with randomly - and is actually intentionally inaccurate - like not how a sphere would be lit in real life — lunarean.”
calcTheta Function
// direction of light source
function calcTheta(x, y) {
if (isJourney) {
return journeyTheta + journeyNoise * noise(x, y);
} else if (isCompass) {
return (int(1000 * noise(1000 * x, 1000 * y)) * TWO_PI) / compassSides;
}
return atan2(0.5 - y, 0.5 - x);
}
Theta considers the mode (Journey, Compass, or Nest to produce a specific type of lightning source. This function is called for each circle.
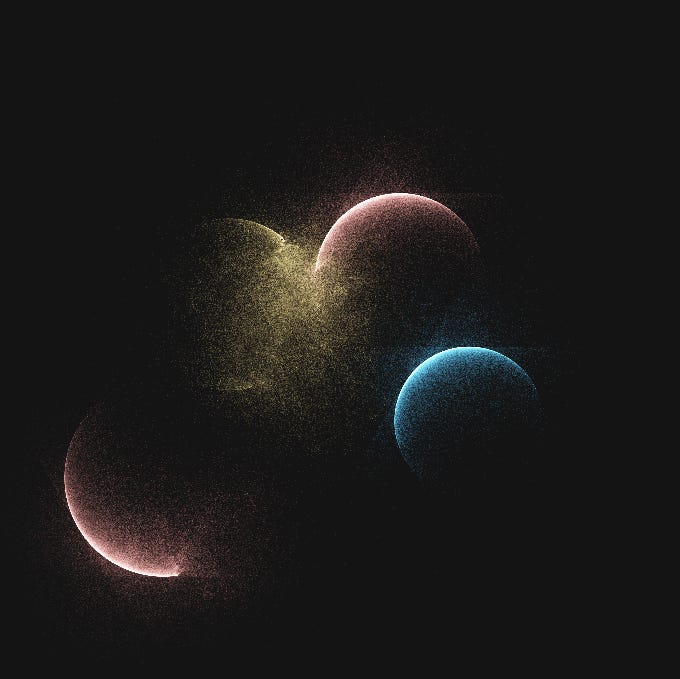
Draw Function
function draw() {
for (let i = 0; i < 12000 && circles.length > 0; i++) {
drawPoint(circles[0]);
if (--circles[0].pointsLeft <= 0) {
circles.shift();
}
}
if (circles.length === 0) {
noLoop();
fxpreview();
}
}
The draw function is straightforward as it loops through the circle’s array calling drawPoint for each element. After each circle is processed, it removes the element from the array.
Instead of drawing each planet (or iterating in the planet’s array alone), the algorithm draws 12000 points at once, which could be part of one planet or spread across multiple. This way, it is much smoother than drawing each planet individually.
Once there aren’t elements in the array, the noLoop() method is called, thus stopping the drawing loop and executing the fxpreview() to produce the output cover.
I hope this was as useful to read as it was for me to write and learn. I believe there are some fundamental techniques we can all learn from lunarean’s setup. This is also a great way to understand how complex this collection (and many gen art projects) can be. In this case, lunarean did a terrific job keeping the code simple and well structured while using best practices to accomplish optimal performance on many fronts.
Thanks to lunarean for the fantastic project, for sharing his knowledge, and for making this open source!
Until next time,
- Kaloh